Introduction

The aim of this classification is to provide quantitative geometrical information on bending properties of nucleic acid double helix structures adopting a uniform analysis approach. The notion bending is used to indicate any global deviation from a straight helix axis. An abrupt local alteration of the helix axis direction is called a kink. The helix axis can, however, also show a smooth bending. Bending can be either an intrinsic property or may be enforced by outer factors like proteins or other ligands, crystal packing, asymmetric charge neutralization of backbone phosphate groups, cation/anion localization or crosslinking. Bending is in any case reflected in local base or dinucleotide step parameters, like roll and tilt angles.

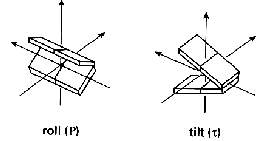
However, this local analysis is not sufficient. Local variations may cancel each other and result in a straight helix axis. Therefore, a thorough bending analysis of nucleic acid double helix structures has to include both the local and global point of view.

More information on geometrical nucleic acid helix parameters can be found here.

Method

The Double Helix/ Bending Analysis web tool included in the IMB Jena Image Library of Biological Macromolecules offers information on local and global helical parameters. The parameters provided include selected information on base step geometries and on backbone conformations and groove widths. In addition, full outputs from the programs CURVES [1] and FREEHELIX [2] are available. For the global bending analysis the helical axis is first determined with the CURVES algorithm [1]. The nucleic acid structures are then oriented in such a way that the coordinate axes are parallel to the principal axes of inertia of the curvilinear helical axis. This results in an immediate visual impression on helix axis bending. Subsequently, the following geometrical models are fitted to the helical axis.
 
 

The definition of the geometrical parameters is described here. Fitting is done with the program ARC_FIT written by P. Slickers. The most appropriate models are selected according to the goodness of fit sigma2.

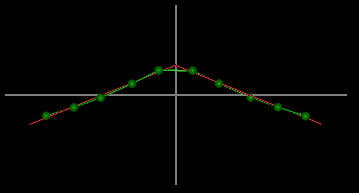
It is important to note that a structure with a helical axis of the type shown in the image is classified as a single-kink duplex.

The Data Set

The analysis is currently done for more than 1201 nucleic acid double helix structures with at least six base pairs. They include free nucleic acids, nucleic acid-protein complexes and complexes of nucleic acids with small ligands. The global shape of the helical axis is a rather crude geometrical measure. We have therefore included high and low-resolution diffraction structures and, in addition, model and NMR structures. Given for NMR structures more than one model is provided only the first model is included in the analysis. Z-DNA structures (Nucleic Acid Database code: z.....), unusual nucleic acids (Nucleic Acid Database code: u......) and further structures with one or more nucleotides in syn conformation are not taken into account. A few additional unusual structures have been removed manually. A complete listing and structure compilations listed by base pair number and protein type can be found here. The database us updated on a regular basis.

Limitations

• For a reliable fitting the number of independent parameters that have to be determined must be smaller than the number of data points (base pairs). Therefore, circular and kinked lines cannot be fitted to a structure with 6 base pairs. For a double-kink line structures with at least 13 base pairs are required. This has the following consequences: It may happen for nucleic acid duplexes with up to 12 base pairs that their helical axis cannot be described by a circular or a single-kink line. They are classified as linear even if the helical axis exhibits marked deviations from a straight line. Structures of this types have a relatively high value of the goodness of fit (examples: 315d, 1qda).
• For structures with 13 or more base pairs it may happen that two kinks occur at neighbouring base pairs or are separated by only one pair. This means that the central segment of a double-kink line consists of zero or one base pairs. In this case a reliable fitting of the central segment is not possible and the kink and twist angles of the double-kink model make no sense (example: 1qp7). These structures have been classified manually in almost all cases as single-kink structures. For the quantitative description of the extent of bending the kink angle of the single-kink line has been used.
• The structures classified as other have goodness-of-fit values larger than 2 for the best model and thus cannot be described by the above-mentioned geometrical models. Nevertheless, the overall shape of most of these structures be approximately described by one of these models given the goodness-of-fit criterion is relaxed. An example is the double-kink line description of the integration host factor/DNA complex (1ihf).
• The goodness of fit may be similar for different models. Therefore, the complete data set has been subdivided into two sets: one for which the most appropriate model of the helix axis has a significantly different goodness of fit as compared to the other competing models (> 0.2) and one for which these difference is smaller (< 0.2). In the latter case the results for the next best models are given in the Tables as well. These structures are included in Tables 2 of the respective classification (straight line, circular line, single-kink line, and double-kink line). In the circular line case the next best model is primarily the single-kink model. For the single-kink line case the next best model is in almost all cases the circular line. This means that most of the structures included in Tables 2 of the circular line and the single-kink line classification could also be merged into one group for which a single-kink line or a circular line are equally suitable for a description of the helical axis.

  
   

   

Bending Classification of Nucleic Acid Double Helix Structures

• Classification by geometrical shape of the helical axis

The following classification is done according to the geometrical shape of the helical axis. Structures with a goodness-of-fit value > 2 are categorized as other. Note that this classification is inevitably arbitrary to some extent.

177 (straight line model is significantly better than any other model) a)

136 (straight line model is only slightly better than other models)

313 (total)

 56 (circular line model is significantly better than any other model)

295 (circular line model is only slightly better than other models)

351 (total)

 60 (structures with 13 or more base pairs) 

233 (structures with 12 or less base pairs)

293 (total)

119 (double-kink line model is significantly better than any other model)

 92 (double-kink line model is only slightly better than other models)

211 (total)

 33

1201 (total)

a) Among these structures there are 159 duplexes with 6 base pairs. In this case no other model than a straight line can be fitted.

• Classification by extent of bending

Contrary to the bending classification given above the following classification is done taking into account the extent of bending alone independent of the appropriate models describing the helical axis. The following generalized measure of bending M has been used:
 
 

The bending class no bending is identical to the straight-line case described above.
 
 

classification I:     322
classification II:    322

classification I:     208
classification II:    226

classification I:     535
classification II:    580

classification I:     136
classification II:     73

total                1201 

classification I 
(sum of kink angles for the double-kink model)
     version A 
     version B
classification II
(largest kink angle for the double-kink model)
     version A
     version B 

total                1201

References

1. Lavery R, Sklenar H, J Biomol Struct Dyn 1988 6: 63-91
2. Dickerson RE, Nucleic Acids Res 1998 26:1906-26.

JenaLib Home| Helix/Bending Analysis Home| Nucleic Acid Bending Classification Home

Biocomputing Group, Leibniz Institute for Age Research - Fritz Lipmann Institute (formerly known as Institute of Molecular Biotechnology), Jena / Germany
All tools for analyzing individual structures were developed by Peter Slickers.
The bending classification was done by Kristina Mehliß and Jürgen Sühnel with support from Jan Reichert and Friedrich Haubensak.