Help

Helical parameters    1. The table of inter base pair parameters    2. The plots of inter base pair parameters    3. Further considerations         Global versus local         Inter base pair parameters         Differences between CURVES and FREEHELIX         Are base pairs planar         Do base pairs stack on each other    Close window

Helix and bending analysis of nucleic acid double helix structures

1. The table of inter base pair parameters

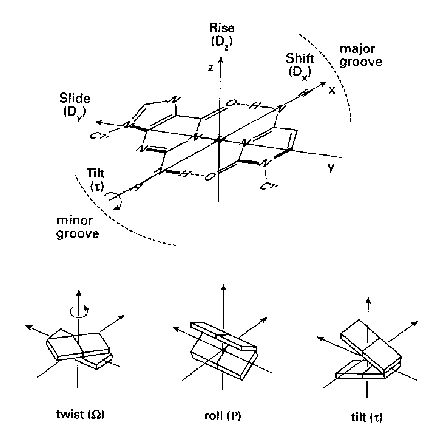
The architecture of a nucleic acid double helices can be described in terms of helical parameters, which have been defined in the Cambridge convention (Dickerson, 1989). The helical parameters are derived from the spatial location of the bases, while the sugar phosphate backbone is not taken into account. The six inter base pairs parameters (rise, twist, shift, roll, tilt, slide) describe the local conformation of a double helix at every base pair step. A table of the inter base pair parameters calculated with respect to the curvilinear helical axis is presented on the 'Analysis of nucleic acid double helix geometry' page. These parameters are calculated with CURVES.

2. The plot of inter base pair parameters

You can also request a plot of the six inter base pair parameters. These plots show three sets of the inter base pair parameters calculated with different approaches:

• CURVES inter base pair parameters calculated with respect to the global helical axis (black lines). These data are also given in the table of inter base pair parameters.
• CURVES inter base pair parameters calculated with respect to the local axes of each dinucleotide step and averaged for the two strands (red lines).
• FREEHELIX vector inter base pair parameters calculated with respect to the local axes of each base pair step (red lines).

Furthermore, also the dinucleotide irregularity function (DIF) from CURVES and the angle between base pair normal vectors from FREEHELIX are shown in the plot. Both graphs are useful to reveal at which base pair step the helix geometry is distorted.

Local distortions of the helix geometry do not necessarily result in a global bending of the helix. A helix is straight, if the helical parameters are regular, but also if all local distortions cancel each other. Bending occurs, if there is either a single local distortion or if various local distortions add up to a global effect. It is intended that users compare the table and the plot of the helical parameters with the images and the geometrical parameters of the helical axis obtained from the 'Bending of the helical axis' page. To facilitate such comparisons the 5'-end of strand 1 is always located at the left hand side, as well in the plots of helical parameters as in the front views of a helix or a helical axis. Accordingly, the 3'-end of strand 1 is always found at the right hand side. This is also the usual way of writing the sequence of a nucleic acid.

The helical parameters are vector quantities characterized by magnitude and direction. They point into different directions at each base pair step. The graphs show only the magnitude of these vectors. If you want to reveal the effect of a distortion of a single helical parameter on the global shape of the helix, you have to take into account also the magnitudes and the directions of all other helical parameters.

3. Further considerations

The terms global and local are used with two different meanings in the field of nucleic acid structure analysis. A global property of a molecular structure depends on all the atoms in the structure, while a local property arises if only a subset of neighboring atoms is used to determine that quantity. In this sense Lavery and Sklenar (1988) have defined global and local helical parameters, which both can be calculated with their program CURVES.

The global as well as the local inter base pair parameters are related to particular base pair steps. These parameters are vector quantities which have a defined location in 3-dimensional space and with respect to the nucleic acid sequence. In contrast, the average inter base pair parameters are scalar values which are not related to any part of the structure. They characterize properties of the whole structure. Confusingly now, the terms local and global are also used to indicate the scope of a property. Local parameters are related to parts of a structure while global parameters are valid for the whole structure. In this sense the global helical parameters from CURVES are also local.

Inter base pair parameters

In Figure 1 the base pairs are shown as planar plates. In a regular helix such planar elements are stacked on each other. Each step from one plate to the next can be described as a combination of a translational and a rotational movement. The translational and the rotational displacements are 3-dimensional vectors, which can be split into three orthogonal components. The three translational components are rise, shift and slide. Rise is a translation in the direction of the helical axis (z-axis), and shift is orthogonal to the helical axis and directs to the major groove side.

Twist, roll and tilt are the three rotational components. Twist is a rotation about the helical axis (z-axis). A positive roll indicates that there is a cleft between two stacked base pairs which opens towards the minor groove. A negative roll is related to an opening towards the major groove. The definitions of the six inter base pair parameters are rigorous but the Cambridge convention does not define how to establish the reference coordinate system. The decomposition of the total translational and rotational movement into orthogonal components depends crucially on the reference system used. Several different algorithms and programs exist for calculating the helical parameters. The algorithms differ mainly in the methods used to derive the reference coordinate systems.

Differences between CURVES and FREEHELIX

In general, most programs in the field yield similar results for regular B-DNA, but the differences are more pronounced for irregular helical stretches. Irregular helices are especially interesting because they occur in several DNA/protein complexes and also in unusual DNA structures like Holliday junctions and other intermediates of DNA recombination. The interpretation of such structures crucially depends on the method used to determine the helical parameters.

One of the merits of the CURVES approach is that it establishes a global helical axis for the whole structure. An optimization procedure is used to determine the best curvilinear axis. The coordinates of the atoms of all bases are employed simultaneously to determine this axis. In this sense CURVES calculates global helical parameters for every base pair step. Other approaches like FREEHELIX determine local helical parameters, where only the coordinates of the two base pairs involved are taken into account. When comparing helical parameters obtained from different methods we must always keep in mind that these parameters are vector quantities. The vectors will differ not only in their lengths but also in their directions.

CURVES can also determine local helical parameters. But these local parameters are different from the local parameters of FREEHELIX. FREEHELIX first fits planes to every base pair and then calculates the helical parameters between the planes. In this way averaging between the two strands is done first. CURVES calculates helical parameters separately for each strand and then does a pairwise averaging of all the parameters resulted for each strand.

If you want to compare two structures you should use helical parameters which have been determined with the same method. Helical parameters found in the literature have often been calculated with different programs or with different program options. Our helix analysis allows to obtain helical parameters calculated with a standardized method for all nucleic acid double helix structures deposited in the PDB and NDB.

Are base pairs planar?

The base pairs in nucleic acid structures are not really planar. For example, the propeller twist of AT base pairs in B-DNA is usually in the range of -15° to -20°. If the base pairs are not planar, the six inter base pair parameters will give only a rough model of the helix. A more detailed picture is obtained if also the intra base pair parameters are taken into account.

The Cambridge convention defines six base pair parameters which describe the deviation from planarity within a base pair (Figure 2). These six parameters describe the translational and rotational displacement between the two bases of a base pair. Again, the translational and rotational displacement is divided into orthogonal components. The translational components are stagger, stretch and shear, and the rotational components are propeller twist, buckle, opening. Instead of determining the (intra) base pair parameters, it is also possible to calculate the inter base pair separately for each strand. Both approaches yield twelve parameters for each base pair.

Do base pairs stack on each other?

The FREEHELIX approach (Dickerson, 1998) is based on the assumption that base pairs are the building blocks of a helix. The base pairs stack on each other to form a helix. Deviations from parallel stacking can be easily detected from the angle between base pair normal vectors. Dickerson has shown for some DNA/protein complexes that local unstacking of base pairs is related to global bending of the helix.

However, if the base pairs deviate significantly from planarity the FREEHELIX method of fitting a common plane to both bases becomes questionable. For non-planar base pairs it seems to be more important how the bases in each strand are stacked on each other. CURVES allows to calculate the inter base pair parameters separately for each strand. If you are interested in these parameters you can request the full output from CURVES and also from FREEHELIX on the 'Analysis of nucleic acid double helix geometry' page. The output files also show precisely which program options are used.